滚轮缩放图表

做过的东西没多久就要忘记。还是写一写吧。最近为了练习原生js、ES2015，写一个线图chart。

滚轮缩放原理很清楚，对应放大-缩小就可以了。具体实现的过程还挺有趣的。

对于图表来说，即改变一下数据-图形的映射关系。再查查MDN上wheel event：

文中也给出了浏览器兼容方案。MDN还有一篇文章详述各浏览器值的不同：https://developer.mozilla.org/en-US/docs/Web/Events/mousewheel。

不考虑兼容性，按着这样简单的原理和愉快的API，按着demo中前面select放大的方式随便写了一个。然后发现了一个问题：

错误缩放示例

功能是实现了，但是不太对劲啊。

哪里不对劲呢？没按鼠标指针所在位置缩放。

果然随便写一个不行了。那搞个方程吧……~！@#￥%……&*好了！

（此处有一个丑得不好意思出场的方程……其实我已经找不到了，大概思路是鼠标指针前后加加减减。）

看来，偷懒是不行的。让我们认真思考一下问题：这是一个怎样的映射关系？现在我才发现我还没描述出这个问题。可能因为这个demo中思维惯性的缘故，问题被我带到了歪路上。所以让我们回到正轨：问题是什么？

先说一下现在的关系：

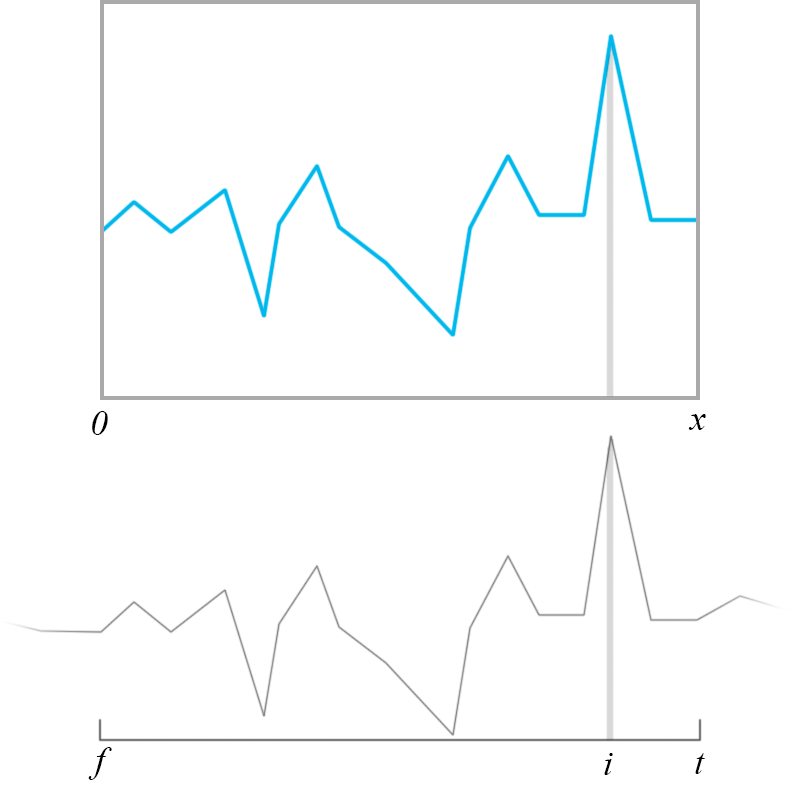映射关系示意图

上图为canvas，下图为data。即f对应图形起始位置0，t对应结束位置x。图形-数据间隔比例s：

$$s=\frac{x}{t-f}$$

如果以px作为canvas单位，s即每个data的px数量。

那么目标是什么呢，目标是缩放时以指针为中心。如何把它转换为一个数学问题？

当然其实上图已经示意了，我也不记得我之前想到了什么邪路上去……关键即图中鼠标指针位置上的data[i]。

转换一下表述就是：在不同s下，保持data[i]在图形上的位置不变。

$$(i-f)\cdot s=(i-{f}')\cdot {s}'$$

如此问题就明晰了。你看问题没什么难度，但是偷懒不提就误入歧途了。

更进一步的：其实只要放大、缩小s就可以了，即加一个ratio r：

$$s={s}'\cdot r$$

整理得：

$${f}'=i-i\cdot r+f\cdot r$$

$${t}'=i-i\cdot r+t\cdot r$$

简单对称美。不过具体到实践中，i仍然需要通过计算得出，重复计算了。我们能获取的是mouse的X。令其为$x_{0}$。进一步推导得：

$${f}'=f+(1-r)\cdot \frac{t-f}{x}\cdot x_{0}$$

$${t}'=t-(1-r)\cdot \frac{t-f}{x}\cdot (x-x_{0})$$

显然$(1-r)\cdot \frac{t-f}{x}$计算一遍就可以了。

于是问题就是这样了。代码还是列一列：

let tmp = (1 - ratio) * (t - f) / canvasWidth;  
let left = f + tmp * (event.offsetX);  
let right = t - tmp * (canvasWidth - event.offsetX);

至于放大还是缩小，只要取ratio的倒数就行了。其实从这个式子里可以看到，直接这么想也可以→_→

不过只要是正确的就是等价的，从哪里入手都没关系。给渣留了无数路……这就是数学的妙处吧。

正确缩放示例

启发是什么呢，启发是……初中数学要学好……

当然啦，先得提出问题！

Yuqian Ma